[Note. This is a slightly modified version of an article that originally appeared in the December 2010 issue of Archive magazine.]
When I started to prepare a talk on this subject for the Midlands User Group last year, my first thought was to base it on an article that I wrote for Archive 17:3 in 2003. However, I quickly realised that the old article would need to be updated, and I added some new material. The present article is an extended version of the talk that I gave.
Cryptology is a broader subject, consisting of two branches: cryptography, the science of creating secure cryptosystems for converting data into a form that is unintelligible to unauthorised persons, and cryptanalysis, the science of 'attacking' cryptosystems in order to 'crack' them or at least discover their weaknesses.
When cryptanalysis reveals weaknesses in cryptosystems, cryptographers create more secure cryptosystems. Conversely, as cryptosystems become stronger, cryptanalysts try to discover more powerful methods of attacking them. Thus, cryptography and cryptanalysis are complementary.
The aim of cryptography is to convert any data in its original form, called the plaintext, into an incomprehensible form, known as the ciphertext. This process is called encryption. The reverse process of recovering the plaintext from the ciphertext is called decryption. In popular writing, one often finds the (incorrect) terms 'encoding' and 'decoding', but technically these have quite different meanings and should not be used in the present context.
It is important to understand that the plaintext need not necessarily be a textual message. It can be a computer file representing any type of date - an image, a database, etc.
Any particular cryptosystem is based on specific encryption and decryption algorithms. An algorithm is simply a computational procedure that follows some specific set of rules. An important general principle of modern cryptography, known as Kerckhoffs' Principle, is that the the algorithms defining a cryptosystem should be publicly known. Only then is it possible for the cryptosystem to be critically analysed by experts, so that users can have confidence in it.
The precise way in which the plaintext is encrypted by means of a specific algorithm depends on a secret key, which in practice is simply some large number. The implication of Kerckhoffs' Principle is that the security of the encryption relies on the secret key, and not on some secret encryption algorithm. It is easy to understand this by means of the following analogy: There are no secrets about how a combination padlock works - its mechanism is designed to open the lock when a particular sequence of numbers is dialed - but a locked padlock is secure because there are typically over a million possible combinations ('keys').
Modern cryptosystems can be classified broadly into two main types: symmetric and public-key cryptosystems. These will be described below.
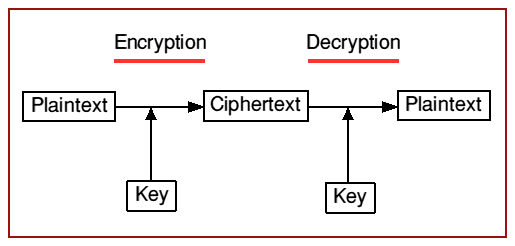
Typically, symmetric encryption is performed by means of a block cipher, which is an encryption method that divides the plaintext into blocks of some fixed length and transforms each block according to a particular algorithm to produce a ciphertext block. The same algorithm and the same key are used for decryption, which reproduces the original plaintext. This is illustrated in figure 1:

An iterated block cipher consists of several successive rounds. Each round carries out the same transformation, using a subkey derived in some way from the original input key.
An important example of an iterated block cipher is the Advanced Encryption Standard (AES), which in 2000 was chosen by the National Institute of Standards and Technology (NIST) in the US as a replacement for the older DES (Data Encryption Standard), which is now considered insecure.
The AES cipher works with blocks of 128 bits and allows key sizes of 128, 192 or 256 bits. Depending on which of the three key sizes is used, there are 10, 12 or 14 rounds. The US government has declared AES acceptable for protecting classified information up to 'top secret', when used with the largest key size (i.e., AES-256).
This cipher, like several others now in common use, is secure against all known methods of cryptanalysis. In particular, there is no known method of cracking it that is more efficient than 'brute force', i.e., testing all possible keys until the right one is found, which in turn is infeasible with any known technology. This is what makes the cipher strong, and it allows us to obtain a quantitative estimate of its strength.
To get some idea of how strong such a cipher is, let us estimate how long it would take, using brute force, to crack AES-128. With 128-bit keys, the number of possible keys is 2128, which is roughly 3×1038. (If you don't know how to convert a power of 2 mathematically to a power of 10, most modern calculators can do this for you.) That's a colossal number, but we still need some assumption about the available computing power in order to arrive at a definite estimate.
Let us be generous and assume, for the sake of definiteness, that we can use 1010 (i.e., 10 billion) computers, each testing 1010 keys per second, so that in total we can test 1020 keys per second. Then the time required to test all possible keys will be (3×1038)/1020=3×1018 seconds, which is about 1011 (i.e., 100 billion) years. This is longer than the known age of the universe, 13.7 billion years, according to modern cosmology. To be fair, on average it would take only half that time to find the right key.
Note that brute force applied in this way would only allow one particular key to be determined. It does not provide a method of cracking the cipher in general, i.e., it is not a method of true cryptanalysis.
With each additional bit in the key length, the number of possible keys is doubled. Suppose, for example, that we use keys with 256 bits instead of 128. How much longer would it then take to crack an encrypted message, under the same assumptions about the available computing power? Using the same method as above, it is left as an exercise for the reader to check that the answer is about 3×1049 years. That is about 300 trillion trillion trillion times longer than for a 128-bit key, which you will probably agree is pretty good security!
Public-key cryptography solves this conundrum neatly. In public-key cryptography, each user has a unique pair of keys: a public key and a secret key.
A public key can be widely publicised and used by anyone to send an encrypted message to the owner of that key, in much the same way that most people publicise their telephone number in a public directory, to enable others to contact them. For example, my public key is available from my personal website, and anyone who knows my name and/or e-mail address can also download it from various public keyservers on the internet.
The secret key is kept strictly secret and can be used (only) by its owner to decrypt messages intended for that particular person. In practice, the secret key is kept strongly encrypted in the user's computer by means of a symmetric cipher. Only the owner of the secret key can unlock it by entering a secret passphrase whenever the encryption program requires that key, after which it is immediately re-encrypted automatically.
The general scheme of public-key cryptography is illustrated in figure 2:
Here Bob is sending a secure message to Alice. It is conventional in such examples to use certain names beginning with A, B or C, as required, and I am also following a popular (non-sexist!) convention that the sender is assumed to male, and the recipient female.
Thus, Bob encrypts the plaintext with Alice's public key (PK), and the resulting ciphertext can be transmitted over an insecure channel such as e-mail. Alice decrypts the ciphertext with her secret key (SK), to recover the original plaintext. Nobody else can do this, because nobody else has access to Alice's secret key.
A simple analogy is again helpful here. The public key is like a combination padlock - anyone can lock it. The secret key is like the combination required to open the padlock - only its owner can do that.
For such a scheme to work, several conditions must be satisfied:
The sender and recipient must use the same (public) encryption/decryption algorithms. Users (more precisely, their encryption software) must be able to generate random key pairs (PK and SK) reasonably efficiently, though this normally needs to be done only once, because each user can continue to use the same key pair. The encryption and decryption processes must be computationally efficient. The SK must decrypt any message encrypted with the PK. And finally, computation of the SK from a knowledge of the PK must be infeasible. This last requirement is what makes the cryptosystem secure.
Since the SK must reverse the action of the PK, these two keys must clearly be mathematically related. It might seem paradoxical at first sight that it is impossible in practice to reverse the action of the public key by deducing the secret key.
The basic mathematical idea that makes such a cryptosystem possible is known as a trapdoor one-way function. A one-way function is a rule for performing a calculation that is easy, but whose inverse is hard to compute. The terms 'easy' and 'hard' here have very specific technical meanings. Roughly speaking, a calculation is 'hard' if (and only if) the time required for a computer to perform the calculation increases exponentially with the size of the input number.
An example of a one-way function is the multiplication of two large prime numbers. Even if the numbers have a few hundred digits each, a modern computer can calculate their product in less than a second, assuming, of course, that it is provided with special routines for dealing with very large numbers. However, if one is given only the product of two such large prime numbers and is asked to recover the two factors, no known computer would be able to solve this problem in less than a million years. Mathematicians generally believe that this is a truly 'hard' problem in the technical sense, although there is at present no strict proof.
A trapdoor function is a one-way function whose inverse becomes 'easy' to compute when certain additional information is known. As a simple example, if the sum of the two prime numbers in the above example is known, it then becomes easy (indeed, trivial) to find the two individual prime numbers. This is the case because it is easy to find two numbers if their sum and product are both known, as anyone who knows elementary algebra can easily verify.
All public-key cryptosystems are based on particular one-way trapdoor functions, including the one explained just above. In any such cryptosystem, the secret key serves as a trapdoor - a special piece of information that makes it possible to reverse the encryption process.
Without much more maths, it is impractical to explain exactly how a pair of public and secret keys can be generated. In fact, this depends on the particular cryptosystem that is used. However, the simple example involving two prime numbers explained above should convince the reader that trapdoor one-way functions are actually possible.
Public-key cryptography is implemented in two types of computer program: PGP (which stands for Pretty Good Privacy) and GnuPG (which stands for GNU Privacy Guard, sometimes also called GPG). These are the worldwide standard for secure e-mail. PGP was the original software, and GnuPG was developed later, but the two are generally interoperable, and versions exist for all major operating systems.
Suppose, once again, that Bob wishes to send a secure message to Alice. Then Bob encrypts the message M using a symmetric cipher, with a randomly generated one-time key K, to obtain the ciphertext M'. At the same time, he encrypts the key K using a public-key cryptosystem, with Alice's public key, to obtain the encrypted key K'. Bob then sends both M' and K' to Alice. This is secure, even over an insecure channel like e-mail.
Alice simply reverses the process in order to read the message. She first decrypts K' using her secret key, to obtain the original key K for the symmetric cipher. She then uses this key K to decrypt the ciphertext M', to obtain the original message M. Of course, both parties must use the same two cryptosystems for this to work.
PGP or GnuPG takes care of all this automatically. In practice, users need not worry about the details of the encryption and decryption processes. Bob's software will be configured to use particular cryptosystems by default (which he can override if desired). His 'public keyring' file will contain the public keys of all his correspondents, and he only needs to specify to whom the encrypted message is to be sent. Alice's software recognises automatically which cryptosystems have been used to encrypt Bob's message, and she only needs to enter her secret passphrase to enable her software to unlock her (encrypted) secret key in order to decrypt Bob's message. PGP or GnuPG enables the users to do all this without much effort.
The dual system has several advantages. As already mentioned, public-key cryptography is less efficient than symmetric cryptography. However, since the public-key cryptosystem is used only to encrypt the key for a symmetric cipher, which is of fixed length (typically between 128 and 256 bits), a modern computer can do this very quickly, regardless of how long the actual message is.
The dual system also means that the same message can be encrypted for multiple recipients very efficiently. It is encrypted only once with the one-time key K, as discussed above, and the sender encrypts this key with each recipient's public key in turn. The whole set of encrypted keys K' is then sent simultaneously to all the recipients, and their software automatically selects the appropriate encrypted key K' in each case. Thus, it is just as easy to encrypt a message simultaneously for multiple recipients as it is to send them a common e-mail using any mail client. The sender merely specifies to which recipients the mail is to be encrypted, and the PGP or GnuPG software takes care of everything.
An interesting consequence of the dual system is that if the same message is encrypted repeatedly, the encryption will be different each time, since a new randomly generated one-time key is used each time for the symmetric cipher.
All versions of GnuPG are freeware and open-source, with no restrictions on their use. They may even be used freely for commercial purposes. The RISC OS port of GnuPG is reasonably up to date and is therefore recommended for RISC OS users. GnuPG (like the old PGP 2) is only a command-line program, and some people find it difficult to remember the correct commands. However, this is not a real problem, because there are excellent front ends for GnuPG (as there are for PGP 2).
Information about PGP and GnuPG for RISC OS, the software itself, and user-friendly front ends can all be obtained from my website at http://www.queen.clara.net/pgp/acorn.html, where visitors can also find guides and tutorials for beginners.
Some popular e-mail clients (for example, Messenger Pro and Pluto) have user-friendly options for secure e-mail using PGP or GnuPG. The use of these options is quite intuitive. I urge all RISC OS users to adopt GnuPG and to persuade all their correspondents to use PGP or GnuPG if they do not already do so. Why send e-mail as plaintext when it takes no more than a second to encrypt or decrypt a typical message, and you can be confident that your correspondence is totally private?
Estonian
translation of this page (provided by Karolin Lohmus)
Russian
translation of this page (provided by
ResumeCoversCV)
Ukrainian
translation of this page (provided by
Open Source Initiative)